| Copyright | (C) 2023-2025 Alexey Tochin |
|---|---|
| License | BSD3 (see the file LICENSE) |
| Maintainer | Alexey Tochin <Alexey.Tochin@gmail.com> |
| Safe Haskell | None |
| Language | Haskell2010 |
| Extensions |
|
Numeric.InfBackprop.Tutorial
Description
Tutorial for the inf-backprop package.
Synopsis
Quick Start
Basic Examples
>>>import GHC.Base (Float, fmap, ($))
In this section, we'll explore how automatic differentiation transforms ordinary mathematical functions into their derivatives, handling everything from basic polynomials to complex compositions without requiring manual derivation.
We'll start by exploring automatic differentiation through the familiar square function:
\[ f(x) := x^2 \]
To work with our automatic differentiation system, we need operations that can handle not just numbers, but also the dual numbers that carry derivative information. The polymorphic multiplication operator from numhask provides this flexibility:
>>>import NumHask (Multiplicative, (*), (+), log)
The operator (*) has the following type signature:
(*) :: Multiplicative a => a -> a -> a
This polymorphic operator allows us to write functions that work seamlessly with both regular numbers and the extended number types used in automatic differentiation.
Let's define our square function and see it in action with regular Float values:
>>>f x = x * x>>>fmap f [-3, -2, -1, 0, 1, 2, 3] :: [Float][9.0,4.0,1.0,0.0,1.0,4.0,9.0]
Now comes the remarkable part: computing the derivative automatically. The
simpleDerivative function applies the chain rule automatically, transforming
any function built from differentiable primitives into its derivative function.
We know from calculus that the derivative of \(x^2\) should be:
\[ f'(x) = 2 \cdot x \]
Let's verify this using automatic differentiation:
>>>import Numeric.InfBackprop (simpleDerivative)
>>>f' = simpleDerivative f :: Float -> Float>>>fmap f' [-3, -2, -1, 0, 1, 2, 3][-6.0,-4.0,-2.0,0.0,2.0,4.0,6.0]
Notice how each result equals \(2x\), perfectly confirming our analytical derivative \(f'(x) = 2x\). The values \(-6, -4, -2, 0, 2, 4, 6\) correspond exactly to \(2\) times each input value.
You must provide a type annotation (such as Float -> Float) for the derivative
function. This ensures correct type inference by the compiler and specifies which
numeric type you want to work with.
Computing higher-order derivatives follows the same pattern. Since composing
simpleDerivative twice gives us the second derivative, this demonstrates how
automatic differentiation naturally handles higher-order derivatives through
function composition.
For our square function, the second derivative should be the constant \(2\):
\[ f''(x) = 2 \]
>>>f'' = simpleDerivative $ simpleDerivative f :: Float -> Float>>>fmap f'' [-3, -2, -1, 0, 1, 2, 3][2.0,2.0,2.0,2.0,2.0,2.0,2.0]
Perfect! The constant value 2.0 across all inputs confirms that our second
derivative is indeed the constant function \(f''(x) = 2\).
This approach scales naturally to arbitrarily complex functions. Let's explore how automatic differentiation handles function composition by examining a more intricate example involving logarithms and polynomial terms:
\[ g(x) := \log (x^2 + x^3) \]
We'll use integer powers from the
IntegralPower
module:
>>>import Debug.SimpleExpr.Utils.Algebra ((^))
>>>g x = log (x ^ 2 + x ^ 3)>>>g' = simpleDerivative g :: Float -> Float>>>g 1 :: Float0.6931472>>>g' 1 :: Float2.5
We can verify this result analytically. The derivative of \(\log(x^2 + x^3)\) using the chain rule is:
\[ g'(x) = \frac{d}{dx}[\log(x^2 + x^3)] = \frac{1}{x^2 + x^3} \cdot \frac{d}{dx}[x^2 + x^3] = \frac{2x + 3x^2}{x^2 + x^3} \]
At \(x = 1\):
\[ g'(1) = \frac{2 \cdot 1 + 3 \cdot 1^2}{1^2 + 1^3} = \frac{2 + 3}{1 + 1} = \frac{5}{2} = 2.5 \]
The automatic differentiation result matches our analytical calculation perfectly, demonstrating how the system correctly applies the chain rule even for complex composite functions.
Derivatives for Symbolic Expressions
>>>import NumHask ((*), sin, cos)>>>import Debug.SimpleExpr (variable, simplify, SimpleExpr, SE)>>>import Numeric.InfBackprop (simpleDerivative)
In many cases, it is more convenient to illustrate differentiation using symbolic expressions rather than concrete numeric values. Unlike numeric differentiation, symbolic expressions allow us to inspect, transform, and optimize derivatives algebraically.
We use the simple-expr package to construct and manipulate symbolic expressions.
For example, consider the function:
\[ f(x) := \sin(x^2) \]
We can define it symbolically as follows:
>>>import Debug.SimpleExpr.Utils.Algebra (AlgebraicPower, (^))
>>>x = variable "x" :: SimpleExpr>>>f x = sin (x ^ 2)>>>f x :: SimpleExprsin(x^2)
where SimpleExpr is a symbolic expression type from
simple-expr
Computing the symbolic derivative
\[ f'(x) := 2x \cdot \cos(x^2) \]
is equally straightforward:
>>>f' = simpleDerivative f>>>simplify $ f' x :: SimpleExpr(2*x)*cos(x^2)
The simplify function from
simple-expr
reduces redundant expressions like
*1 and +0.
and presents the result in a more readable algebraic form.
Bellow, we will use the SE type synonym for SimpleExpr.
Note that we continue to use generic definitions of functions like cos,
as well as operators such as (*), from the
numhask
package.
Symbolic Expressions Visualization
The simple-expr package includes visualization tools that help illustrate the process of symbolic differentiation.
>>>import Debug.SimpleExpr (SimpleExpr, variable, simplify, plotExpr, plotDGraphPng)>>>import Debug.DiffExpr (unarySymbolicFunc)>>>import Numeric.InfBackprop (simpleDerivative)
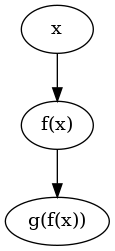
As a warm-up, consider a simple composition of two symbolic functions:
\[ x \mapsto g(f(x)) \]
This can be represented as:
>>>x = variable "x" :: SimpleExpr>>>f = unarySymbolicFunc "f" :: SimpleExpr -> SimpleExpr>>>g = unarySymbolicFunc "g" :: SimpleExpr -> SimpleExpr>>>g (f x) :: SimpleExprg(f(x))
You can visualize this expression using:
plotExpr $ g (f x)
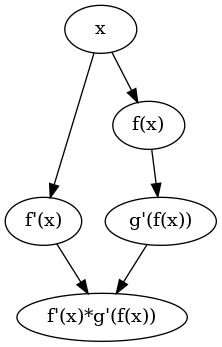
To visualize the first derivative of this composition, use:
plotExpr $ simplify $ simpleDerivative (g . f) x
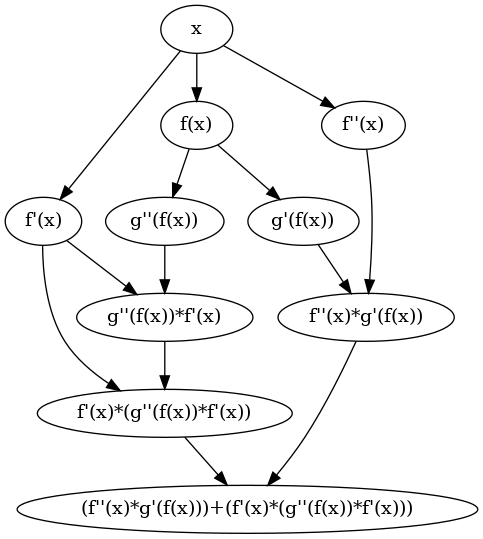
Visualizing the second derivative is just as easy:
plotExpr $ simplify $ simpleDerivative (simpleDerivative (g . f)) x
Gradient over a Two-Argument Function
In this section, we focus on computing partial derivatives of functions with two arguments.
As a starting point, consider a symbolic function h that takes two arguments.
(See
Derivatives for Symbolic Expressions
.)
>>>x = variable "x">>>y = variable "y">>>h = binarySymbolicFunc "h" :: BinarySymbolicFunc a => a -> a -> a>>>h x yh(x,y)
To compute partial derivatives, we use the twoArgsDerivative operator,
which has a somewhat advanced type signature (see Section ??? for details).
In practice, its usage is straightforward:
>>>:{h' :: SE -> SE -> (SE, SE) h' x y = simplify $ twoArgsDerivative h x y :}
This returns a pair of partial derivatives:
>>>h' x y(h'_1(x,y),h'_2(x,y))
We can also compute the second-order derivatives by nesting twoArgsDerivative:
>>>:{h'' :: SE -> SE -> ((SE, SE), (SE, SE)) h'' x y = simplify $ twoArgsDerivative (twoArgsDerivative h) x y :}
>>>h'' x y((h'_1'_1(x,y),h'_1'_2(x,y)),(h'_2'_1(x,y),h'_2'_2(x,y)))
In this example, h'_1'_2 refers to the second partial derivative of h
with respect to x and then y, and so on.
Note that twoArgsDerivative is polymorphic over the return type of the function,
but it works only for functions that take exactly two arguments.
In contrast, the customArgValDerivative autoArg operator
(see
Structured Argument Type)
can handle functions of arbitrary arity, but it is not polymorphic
over the return type of the function.
Siskind-Pearlmutter Example
We are now ready to revisit a classic example of higher-order automatic differentiation from the paper by Siskind and Pearlmutter: Siskind & Pearlmutter (2005), "Perturbation Confusion and Referential Transparency" The expression of interest is:
\[ \left. \frac{\partial}{\partial x} \left( x \left( \left. \frac{\partial}{\partial y} \left( x + y \right) \right|_{y=1} \right) \right) \right|_{x=1} = 1 \]
To implement this, we begin by applying the partial derivative operator
twoArgsDerivativeOverY, which differentiates a binary function
with respect to its second argument:
For example, to compute
\[ \frac{\partial}{\partial y} (x \cdot y) = x \]
we write:
>>>x = variable "x">>>y = variable "y">>>simplify $ twoArgsDerivativeOverY (*) x y :: SEx
To evaluate this derivative at y = 1, we can use the stopDiff function,
which performs symbolic substitution. For instance,
stopDiff $ number 1
effectively replaces y with 1 in the expression.
So the expression
\[ \left. \frac{\partial}{\partial y} (x \cdot y) \right|_{y=1} = x \]
is implemented as:
>>>simplify $ twoArgsDerivativeOverY (*) x 1 :: SEx
Now we can wrap the entire expression in a derivative with respect to x:
\[ \frac{d}{dx} \left. \frac{\partial}{\partial y} (x \cdot y) \right|_{y=1} = 1 \]
This becomes:
>>>:{simplify $ (simpleDerivative $ \x_ -> twoArgsDerivativeOverY (*) x_ 1) x :: SE :} 1
The same logic works not just for symbolic expressions (SE),
but also for concrete numeric types such as Float:
>>>:{simpleDerivative (\x -> x * twoArgsDerivativeOverY (+) x 1) (2024 :: Float) :} 1.0
Note: when working with numeric types like Float,
the variable x must be assigned a concrete Float value.
How it Works
The Backpropagation Derivative
To clarify the concept of backpropagation, consider the following example.
Let h, f, and g be three simple functions of type:
\[ \mathbb{R} \rightarrow \mathbb{R} \]
Now consider their composition:
\[ x \mapsto g(f(h(x))) \]
The first derivative of this composition, using the chain rule, is:
\[ x \mapsto h'(x) \cdot f'(h(x)) \cdot g'(f(h(x))) \]
This composition and its derivative can be illustrated using the following computation graph:

The top path (from left to right) represents the forward pass, where values are computed through the function chain. The bottom path (from right to left) represents the backward pass, where derivatives are propagated.
According to the backpropagation strategy, the derivative is computed in reverse order, as follows:
- Evaluate
h(x). - Compute
f(h(x)). - Compute
g(f(h(x))). - Compute the top derivative:
g'(f(h(x))). - Compute the next derivative:
f'(h(x)). - Multiply:
g'(f(h(x))) * f'(h(x)). - Compute the base derivative:
h'(x). - Multiply the result from step 6 by
h'(x).
The product of these three derivatives gives the full derivative of the composition.
Note: While it is possible to compute this derivative in forward order (i.e., from left to right) or any other order, the backpropagation strategy is more efficient for deep machine learning applications. Forward-mode differentiation is beyond the scope of this library.
Generalizing this approach to longer function chains or functions from and to vector spaces is straightforward and follows the same principles.
Core Type: RevDiff
All the derivative computations from the previous example —
specifically for the function f —
can be conceptually divided into two phases:
- Forward step: Compute the value
f(h(x)). - Backward step:
Compute the derivative
f'(h(x)), and multiply it by the previously obtained derivativeg'(f(h(x))).
Note that the value h(x) is used in both the forward and backward steps.
The corresponding diagram can be visualized as:
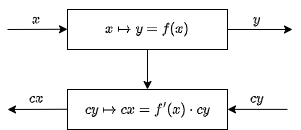
A differentiable function from type a to type b can be represented
as a pair of functions:
a forward function and a backward (derivative propagation) function:
newtype DifferentiableFunc a b = MkDifferentiableFunc {
forward :: a -> b,
backward :: a -> CT b -> CT a
}
The meaning of the CT type family (short for cotangent)
will be discussed in the
next section.
For now, you may assume CT a ~ a.
From a categorical perspective, a DifferentiableFunc behaves like a lens:
DifferentiableFunc a b ≈ Lens a (CT a) b (CT b)
where forward corresponds to view, and backward corresponds to set.
In principle, one could define a category of differentiable functions using lenses,
replacing standard function composition (.) with lens composition `(% or >>>)`.
However, this comes at a cost: we lose the ability to use familiar syntax such as
function application y = f x.
To preserve the familiar function syntax — e.g., keeping definitions like
sin :: a -> a
and supporting ordinary function application — we follow an approach inspired by the
ad
and
backprop libraries.
See also, for example,
this article
Fixing a type t (which plays the role of the final output), we can reinterpret
a lens-like function
dFunc :: DifferentiableFunc a b
as a transformation on differentiable values:
lensToMap :: DifferentiableFunc a b -> DifferentiableFunc t a -> DifferentiableFunc t b lensToMap dFunc = dFunc <<< -- lens composition
So, lensToMap dFunc becomes a plain Haskell function:
DifferentiableFunc t a -> DifferentiableFunc t b
Mathematically, this is a hom-functors from the cathegory of law-breaking lenses.
Next, note that the type
DifferentiableFunc t a
is isomorphic to:
t -> (a, CT a -> CT t)
But the actual value of type t is not used the composion with
DifferentiableFunc a b.
Therefore, we can drop the t parameter and reduce the transformation:
DifferentiableFunc t a -> DifferentiableFunc t b
to a plain function:
(a, CT a -> CT t) -> (b, CT b -> CT t)
This motivates the definition of the core type:
data RevDiff' t a = MkRevDiff
{ value :: a
, backprop :: CT a -> CT t
}
For example, suppose we have a function:
f :: Float -> Float -- function f f' :: Float -> Float -- derivative of f
Then the differentiable version of f can be defined as:
differentiableF :: RevDiff' t Float -> RevDiff' t Float differentiableF (MkRevDiff x backprop) = MkRevDiff (f x) (cx -> backprop ((f' x) * cx))
To evaluate the function at a point x:
y = value $ differentiableF (MkRevDiff x id)
To evaluate its derivative at x:
y' = backprop (differentiableF (MkRevDiff x id)) 1.0
Here, the transition from type a to RevDiff' t a carries two parts:
from type CT a to CT t.
In the example above, the value:
MkRevDiff x id :: RevDiff Float Float
represents the initial value of the backpropagation stack.
Applying differentiableF
results in:
MkRevDiff (f x) (\cx -> id ((f' x) * cx)) = MkRevDiff (f x) ((f' x) *)
So applying backprop to 1.0 :: Float gives us the derivative value f' x.
For convenience and flexibility, this package defines a three-parameter type:
data RevDiff a b c = MkRevDiff {value :: c, backprop :: b -> a}
This generalized structure allows us to separate the types involved in the
forward pass (the value of type c) from those used in the backward pass
(the gradient computation from b to a).
We also provide a specialized type alias for common use cases:
type RevDiff' a b = RevDiff (CT a) (CT b) b
This three-parameter design enables powerful abstraction capabilities. In particular, it allows us to implement both profunctor and Van Laarhoven representations for differentiable functions, providing multiple ways to compose and manipulate automatic differentiation computations.
These alternative representations can be accessed through the conversion
functions fromProfunctors, toProfunctors, fromVanLaarhoven, and
toVanLaarhoven, each offering different compositional properties suited
to various use cases.
Generalizing this to arbitrary compositions of differentiable functions is straightforward and follows the same backpropagation principle.
Functions Overloading
Our goal now is to make functions such as sin and (*) differentiable,
while still being able to use them as ordinary functions — in particular,
to apply them to arguments and compose them using (.).
To this end, we follow the approach used in the
numhask package.
In this package, functions like sin and (*) are defined as polymorphic methods
of typeclasses.
For instance, the function sin is a method of the typeclass:
class TrigField a where ... sin :: a -> a
Similarly, multiplication is defined via:
class Multiplicative a where ... (*) :: a -> a -> a
These typeclasses have instances, for example, for the type Float.
Instancies for SE are provided in
simple-expr
package.
To make sin and (*) differentiable in the backpropagation framework,
it is enough to define instances for:
RevDiff Float Float
These instances can be implemented as follows.
(The type family CT can be ignored for now, we may assume CT a ~ a for simplicity.)
instance Additive (CT t) => TrigField (RevDiff t Float) where
...
sin :: RevDiff t Float -> RevDiff t Float
sin MkRevDiff {value = x, backprop = backpropX} = MkRevDiff {
value = sin x,
backprop = backpropX . ((cos x) *)
}
instance Additive (CT t) => Multiplicative (RevDiff t Float) where
...
(*) :: RevDiff t Float -> RevDiff t Float -> RevDiff t Float
MkRevDiff x backpropX * MkRevDiff y backpropY =
MkRevDiff {
value = x * y,
backprop = backpropX . (y *) + backpropY . (x *)
}
To compute second derivatives, we can use a nested type like:
RevDiff (RevDiff Float Float) (RevDiff Float Float)
That is, the outer layer performs backpropagation through the inner derivative.
Similarly, higher-order derivatives can be obtained by nesting RevDiff types further.
These instances can also be generalized to any numeric type a, not just Float,
allowing us to define infinitely differentiable functions.
Tangent and Cotangent Spaces
In this section, we explain the purpose of the type family CT and how it is used.
In most practical cases, we can assume CT a ~ a and safely ignore it.
One of the challenges in automatic differentiation is that the value type of a function and the value type of its derivative may not coincide, even when the input is scalar (for example, a real number). From a mathematical perspective, this corresponds to the need to work with tangent and cotangent bundles.
For instance, if a scalar-valued function takes a vector as input, its derivative is also vector-valued. However, this correspondence does not hold in general.
Consider the case where the input is an infinite sequence
(such as an infinte list or stream).
The derivative of a function on such inputs is a finite-length sequence
(a sparse or finite-support vector; see the FiniteSupportStream type).
Conversely, a function on finite-support streams has a derivative
that is generally represented as an infinite stream.
This distinction arises because the convolution of two infinite streams is not defined in general. On the other hand, every linear functional on streams can be represented as a convolution with a finite-length vector. Conversely, a convolution with a finite-length vector defines a linear functional on infinite streams.
Similarly, any linear functional on all bounded finite-length vectors can be represented as a convolution with an infinite sequence. And conversely, convolution with an infinite sequence yields a linear functional on finite-length vectors.
These distinctions are not just mathematical formalisms,
but real practical constraints.
In particular, the convolution of two streams cannot be calculated.
In this package, the Haskell type system cannot safely express, for example,
that the derivative of a function over Stream should be of type Stream,
or that the derivative of a function over FiniteSupportStream
should also be of type FiniteSupportStream.
Another example comes from geometry. Consider a function defined on the surface of a unit sphere in 3D space. In this case, the derivative at each point must lie in the tangent plane to the sphere at that point — not just any 3D vector. Therefore, the derivative type differs from the function's output type.
More generally, in differential geometry, functions are defined on manifolds, and their derivatives take values in the cotangent bundle of the manifold.
To model this distinction in Haskell,
we introduce the type family CT, which stands for "cotangent type".
For example:
CT Float = Float
CT (a, b) = (CT a, CT b)
CT (Vector a) = Vector (CT a)
CT (Stream a) = FiniteSupportStream (CT a)
CT (FiniteSupportStream a) = Stream (CT a)
CT (E2NormedVector a) = Vector (CT a)
The type family CT is defined as a composition of two type families:
Tangent and Dual:
CT a = Dual (Tangent a)
The Tangent family describes the type of tangent vectors.
For example:
Tangent Float = Float
Tangent (Stream a) = Stream (Tangent a)
Tangent (FiniteSupportStream a) = Tangent (FiniteSupportStream a)
Tangent (E2NormedVector a) = Vector (Tangent a)
The Dual family encodes the dual space (linear functionals):
Dual Float = Float
Dual (Stream a) = FiniteSupportStream (Dual a)
Dual (FiniteSupportStream a) = Stream (Dual a)
Dual (E2NormedVector a) = Undefined
In order to support differentiation over a new type that is not already
handled by this package, one needs to define appropriate instances
for both Tangent and Dual for that type.
Differentiation for Structured Types
This library supports the differentiation of functions of type
f :: a -> b
for potentially any types a and b.
Thus, the derivative operator has the type:
(a -> b) -> (a -> c)
The argument type a is the same for both the original function
f :: a -> b and its derivative
f' :: a -> c.
However, the result type c of the derivative
depends in a non-trivial way on both a and b.
For example, the derivative of a vector-valued function of a tuple is a vector of tuples:
>>>import Numeric.InfBackprop.Utils.SizedVector (BoxedVector)
f :: (Float, Float) -> BoxedVector 3 Float f' :: (Float, Float) -> BoxedVector 3 (Float, Float)
To illustrate the approach, consider a representative example: a function from a tuple to a 3D vector.
>>>:{sphericToVec :: (TrigField a) => (a, a) -> BoxedVector 3 a sphericToVec (theta, phi) = DVGS.fromTuple (cos theta * cos phi, cos theta * sin phi, sin theta) :}
We will use the customArgValDerivative operator, which takes three arguments:
- The argument structure descriptor — in this case,
tupleArg, which is used for the(a, a)input. - The value structure descriptor — in this case,
boxedVectorVal, used for output typeBoxedVector 3 _. - The function to differentiate — in this case,
sphericToVec.
The derivative is then defined as:
>>>import Debug.SimpleExpr.Utils.Algebra (IntegerPower)>>>:{sphericToVec'V1 :: (TrigField a, ExpField a, IntegerPower a, a ~ CT a) => (a, a) -> BoxedVector 3 (a, a) sphericToVec'V1 = customArgValDerivative tupleArg boxedVectorVal sphericToVec :}
The type family CT and its meaning are explained in section
Tangent and cotangent spaces.
For now, it can be ignored.
The types and definitions of tupleArg and boxedVectorVal,
as well as how to construct them for other types,
will be covered in the following sections.
Alternatively, the argument and value structure can be inferred automatically
using autoArg and autoVal:
>>>:{sphericToVec'V2 :: (TrigField a, ExpField a, IntegerPower a, a ~ CT a) => (a, a) -> BoxedVector 3 (a, a) sphericToVec'V2 = customArgValDerivative autoArg boxedVectorVal sphericToVec :}
>>>:{sphericToVec'V3 :: (TrigField a, ExpField a, IntegerPower a, a ~ CT a) => (a, a) -> BoxedVector 3 (a, a) sphericToVec'V3 = customArgValDerivative tupleArg autoVal sphericToVec :}
Automatically deriving both the argument and value types is often problematic due to type inference limitations in Haskell.
In summary, there are three common approaches to managing types
in the derivative operator for a function f :: a -> b:
- Define a derivative operator specialized for specific types
aandb. - Define a derivative operator that is polymorphic in the result type
b, but has a fixed argument typea. See section Structured Value Type. - Define a derivative operator that is polymorphic in the argument type
a, but has a fixed result typeb. SeescalarValDerivativein the subsection Structured Argument Type.
Structured Value Type
This section explains how to compute derivatives of functions whose values have structured types (e.g., tuples, vectors, streams, or nested combinations).
We begin with basic examples to demonstrate how derivatives work for common structured types.
Then, in custom derivative operators and value structure descriptors, we explain how to define derivative operators for any structured value type using custom descriptors.
In how it works: structured value types, we delve into the type signatures and the underlying idea behind value type descriptors.
Finally, in defining custom differentiable value types, we outline how to define your own differentiable types—beyond the scope of the built-in descriptors provided by this package.
Basic Examples: Structured Value Types
Tuple-valued function
As a first example, we define a symbolic function f of one variable
that returns a tuple of two values.
>>>:{f :: TrigField a => a -> (a, a) f t = (cos t, sin t) :}
Define a symbolic variable t, as shown in the section
Derivatives for Symbolic Expressions.
>>>t = variable "t">>>f t(cos(t),sin(t))
The simplest way to take the derivative is to use the scalarArgDerivative operator,
which is polymorphic over the function's value type.
It is a polymorphic version of customArgValDerivative operator considered
in the beginning of the section
Differentiation for Structured Types
It is defined as:
scalarArgDerivative = customArgValDerivative scalarVal autoVal
The first argument scalarVal indicates that the function's argument type is scalar.
The second argument autoVal tells the system to infer the value type automatically.
The general type signature of scalarArgDerivative is discussed in a later section.
In this case, it simplifies to:
scalarArgDerivative :: Multiplicative (CT a) => (RevDiff a a -> (RevDiff a a, RevDiff a a)) -> a -> (CT a, CT a)
We can now compute derivatives as follows:
>>>f' = simplify . scalarArgDerivative f :: SE -> (SE, SE)>>>f' t(-(sin(t)),cos(t))
>>>f'' = simplify . scalarArgDerivative (scalarArgDerivative f) :: SE -> (SE, SE)>>>f'' t(-(cos(t)),-(sin(t)))
>>>(scalarArgDerivative (scalarArgDerivative f)) t :: (SE, SE)(-(cos(t)*(1*1))+0,(-(sin(t))*(1*1))+0)
>>>temp t = -((cos t)*(one * one)) + zero
- - >>> (scalarArgDerivative temp) t :: SE
>>>import Debug.SimpleExpr.Utils.Algebra ((^))
>>>(scalarArgDerivative (scalarArgDerivative (scalarArgDerivative f))) (0.0 :: Float) :: (Float, Float)(0.0,-1.0)
>>>(scalarArgDerivative exp) t :: SEexp(t)*1
>>>(scalarArgDerivative (scalarArgDerivative (exp))) t :: SE(exp(t)*(1*1))+0
>>>f''' = simplify . scalarArgDerivative (scalarArgDerivative (scalarArgDerivative f)) :: SE -> (SE, SE)>>>f''' t(sin(t),-(cos(t)))
Note that all derivateive function argiment types are the same
as the original function, but the value typea are different.
Here the the polymorphic preoperty of the scalarArgDerivative operator
comes into play, allowing us to differentiate functions without explicit
type annotations.
Vector-valued function
In the next example, we take the derivative of a vector-valued symbolic function v
using boxed vectors from the
vector-sized library.
>>>import Numeric.InfBackprop.Utils.SizedVector (BoxedVector)
>>>:{v :: SymbolicFunc a => a -> BoxedVector 3 a v t = DVGS.fromTuple ( unarySymbolicFunc "v_x" t, unarySymbolicFunc "v_y" t, unarySymbolicFunc "v_z" t ) :}
>>>v tVector [v_x(t),v_y(t),v_z(t)]
>>>v' = simplify . scalarArgDerivative v :: SE -> BoxedVector 3 SE>>>v' tVector [v_x'(t),v_y'(t),v_z'(t)]
Stream-valued function
Other data types, including lazy types such as streams from the stream library, can also be differentiated.
>>>:{s :: SymbolicFunc a => a -> Stream a s t = fromList [unarySymbolicFunc ("s_" <> show n) t | n <- [0..]] :}
>>>take 5 (s t)[s_0(t),s_1(t),s_2(t),s_3(t),s_4(t)]
>>>:{s' :: SE -> Stream SE s' = simplify . scalarArgDerivative s :}
>>>take 5 (s' t)[s_0'(t),s_1'(t),s_2'(t),s_3'(t),s_4'(t)]
4. Nested structured-valued function
We can also differentiate functions returning values in nested types. For example:
>>>:{g :: SymbolicFunc a => a -> (BoxedVector 3 a, Stream a) g t = (v t, s t) :}
This function has the type a -> (BoxedVector 3 a, Stream a).
Automatic differentiation remains straightforward:
>>>:{g' :: SE -> (BoxedVector 3 SE, Stream SE) g' = simplify . scalarArgDerivative g :}
>>>fst $ g' tVector [v_x'(t),v_y'(t),v_z'(t)]
>>>take 5 $ snd $ g' t[s_0'(t),s_1'(t),s_2'(t),s_3'(t),s_4'(t)]
Custom Derivative: Structured Value Types
Instead of the polymorphic scalarArgDerivative operator,
which is defined as
scalarArgDerivative = customArgValDerivative scalarArg autoVal
we can use a more specialized version tailored to the expected value type.
These customized derivatives still use customArgValDerivative with a specific
value structure descriptor but not autoVal.
Tuple-valued function
Consider again the example from the previous subsection:
>>>scalarTupleDerivative = customArgValDerivative scalarArg tupleVal
Here, scalarArg indicates that
the input of the function being differentiated
is a scalar value, and
tupleVal indicates that the output of the function being differentiated
is a tuple of scalar values.
>>>:{t :: SE t = variable "t" f :: TrigField a => a -> (a, a) f t = (cos t, sin t) f' :: SE -> (SE, SE) f' = simplify . scalarTupleDerivative f :}
>>>f' t(-(sin(t)),cos(t))
Vector-valued function
Similarly, we can define a derivative operator for a vector-valued function v:
>>>scalarTupleBoxedVectorDerivative = customArgValDerivative scalarArg boxedVectorVal
Here, boxedVectorVal declares that the function returns a boxed vector
of scalar values.
Nested structured output function
In the third example from the previous subsection:
>>>import Numeric.InfBackprop.Utils.SizedVector (BoxedVector)
>>>:{g :: SymbolicFunc a => a -> (BoxedVector 3 a, Stream a) g = undefined :}
the value type of g is more sophisticated, so we must construct
a custom value structure manually:
>>>tupleBoxedVectorStreamVal = mkTupleVal (mkBoxedVectorVal scalarVal) (mkStreamVal scalarVal)>>>scalarTupleBoxedVectorStreamDerivative = customArgValDerivative scalarArg tupleBoxedVectorStreamVal>>>_ = scalarTupleBoxedVectorStreamDerivative g :: SE -> (BoxedVector 3 SE, Stream SE)
Here:
mkTupleValconstructs a value descriptor for a tuple,mkBoxedVectorValconstructs a value descriptor for a boxed vector,mkStreamValconstructs a value descriptor for a stream,- and
scalarValdenotes the scalar leaf type.
In general, these building blocks combine to define custom value descriptors. For example:
tupleVal = mkTupleVal scalarVal boxedVectorVal = mkBoxedVectorVal scalarVal streamVal = mkStreamVal scalarVal
And for a scalar-valued function, we simply use:
scalarScalarDerivative = customArgValDerivative scalarArg scalarVal
How it Works: Structured Value Types
This section explains how the general backpropagation mechanism operates at the level of function result (value) types.
Derivative Operator Type Signature
To differentiate a scalar-to-scalar function f :: a -> b, we use its
differentiable form:
f :: RevDiff a a -> RevDiff a b
(see the section
How it works: core type RevDiff).
For functions returning structured values, we generalize this to:
f :: RevDiff a a -> c
where c is a structured result built from `RevDiff a b` values.
We then use a value structure descriptor of type c -> d
to extract the final derivative result d from the structure c.
The resulting derivative operator has the following type:
scalarCustomArgDerivative :: (c -> d) -> -- how to extract the final output (RevDiff a a -> c) -> -- the differentiable function (a -> d) -- scalar input to final output scalarCustomArgDerivative = customArgValDerivative scalarArg
Here, the first argument of type c -> d transforms the intermediate structured result
into the final derivative value.
In fact, scalarCustomArgDerivative is simply function composition:
scalarCustomArgDerivative = (.)
Value Descriptor Examples
Common value structure descriptors include in particular:
- Scalar value
scalarVal :: Multiplicative (CT b) => RevDiff a b -> CT a
Converts a single differentiable value into a scalar result.
- Tuple
tupleVal :: (Multiplicative (CT b0), Multiplicative (CT b1)) => (RevDiff a0 b0, RevDiff a1 b1) -> (CT a0, CT a1)
Converts a tuple of differentiable values into a tuple of scalars.
- Boxed Vector
boxedVectorVal :: Multiplicative (CT b) => BoxedVector n (RevDiff a b) -> BoxedVector n (CT a)
Converts a boxed Vector of differentiable values into a boxed Vector of scalars.
- Stream
streamVal :: Multiplicative (CT b) => Stream (RevDiff a b) -> Stream (CT a)
Converts a stream of differentiable values into a stream of scalars.
- Nested structure
For example, a function returning a tuple of a boxed vector and a stream:
tupleBoxedVectorStreamVal :: Multiplicative (CT b) => (BoxedVector n (RevDiff a0 b0), Stream (RevDiff a1 b1)) -> (BoxedVector n (CT a), Stream (CT a))
Constructing Value Descriptors
You can construct value descriptors using standard higher-order functions:
mkTupleVal :: (a0 -> b0) -> (a1 -> b1) -> (a0, a1) -> (b0, b1) mkTupleVal = cross mkBoxedVectorVal :: (a -> b) -> BoxedVector n a -> BoxedVector n b mkBoxedVectorVal = fmap mkStreamVal :: (a -> b) -> Stream a -> Stream b mkStreamVal = fmap
This means that to define a derivative for any custom structured type MyType a,
you only need to implement:
myTypeVal :: Multiplicative (CT b) => MyType (RevDiff a b) -> MyType (CT a)
A typical approach is to define a mapping function:
mkMyTypeVal :: (a -> b) -> MyType a -> MyType b
and then obtain the value descriptor by applying it to scalarVal:
myTypeVal = mkMyTypeVal scalarVal
This approach allows you to differentiate functions returning arbitrarily
nested combinations of types, as we did above with tuple (,),
BoxedVector n, and Stream.
Defining Custom Value Type
Making Custom Scalar Type Differentiable
To make a scalar type a differentiable, it is necessary and sufficient to:
- Define the type families
TangentforaandDualfor `Tangent a` (see Tangent and Cotangent Spaces). - Ensure that the type
type CT a = Dual (Tangent a)
is an instance of Multiplicative.
The second condition is required to initialize the backpropagation process
with the value one.
Making Custom Type Constructors Differentiable
To define derivatives over a custom type constructor f :: Type -> Type,
the recommended approach is:
- Define the value descriptor:
mkFVal :: (a -> b) -> f a -> f b
In most cases, this is just fmap, or an optimized equivalent (see previous section).
- Provide an instance of the
AutoDifferentiableValueclass:
instance (AutoDifferentiableValue a b) => AutoDifferentiableValue (f a) (f b) where autoVal :: f a -> f b autoVal = mkFVal autoVal
This recursively applies autoVal within the structure of f a.
For more sophisticated custom types (e.g. higher-kinded types such as
g :: Type -> Type -> Type), refer to the implementation of the instance for
tuples (,) in AutoDifferentiableValue for guidance.
Structured Argument Type
In this section, we consider how to differentiate a function with a structured or nontrivial argument type.
The simplest way to compute the derivative of a scalar-valued function (i.e. gradient)
is by using the scalarValDerivative operator.
This operator is polymorphic over the function’s argument type,
but it is restricted to functions that return scalar values.
In terms of the more general customArgValDerivative operator
Differentiation for Structured Types,
the scalarValDerivative is equivalent to:
scalarValDerivative = customArgValDerivative autoArg scalarVal
Here, the first argument autoArg indicates that the argument type
(i.e. the structure of the input) is inferred automatically.
The second argument scalarVal specifies that the return value of the function
must be a scalar.
Basic Examples: Structured Argument Types
Gradient over the Euclidean Norm of a Vector
Our first example involves a function over a sized boxed vector,
BoxedVector. We define the squared Euclidean norm of a 3-dimensional vector:
>>>import Debug.SimpleExpr.Utils.Algebra (IntegerPower, (^), MultiplicativeAction)>>>import Numeric.InfBackprop.Utils.SizedVector (BoxedVector)
>>>:{eNorm2 :: (IntegerPower a, Additive a) => BoxedVector 3 a -> a eNorm2 x = foldl' (+) zero (fmap (^2) x) :}
This is not the most efficient way to define a function on large vectors, but for this example, we focus on type signatures and type inference rather than performance.
The gradient of eNorm2 can be computed as:
>>>:{eNorm2' :: ( IntegerPower a, MultiplicativeAction Integer a, Distributive a, CT a ~ a ) => BoxedVector 3 a -> BoxedVector 3 a eNorm2' = scalarValDerivative eNorm2 :}
As usual, scalarValDerivative can be applied to symbolic expressions,
such as values of type SE:
>>>x = variable "x">>>y = variable "y">>>z = variable "z">>>r = DVGS.fromTuple (x, y, z) :: BoxedVector 3 SE>>>simplify $ eNorm2' r :: BoxedVector 3 SEVector [2*x,2*y,2*z]
It also works with numeric types like Float:
>>>v = DVGS.fromTuple (1, 2, 3) :: BoxedVector 3 Float>>>eNorm2' v :: BoxedVector 3 FloatVector [2.0,4.0,6.0]
Gradient over a Stream
The Stream type can also be used as an argument.
However, note that the result of the gradient is not a Stream,
but rather a bounded stream: FiniteSupportStream.
See
Tangent and Cotangent Spaces
for a brief explanation.
Define a formal series
\[ s = s_0, s_1, s_2, s_3, \ldots \]
as:
>>>s = fromList [variable ("s_" <> show n) | n <- [0 :: Int ..]] :: Stream SE
Next, define a function that sums the first four elements of the stream:
\[ s \mapsto s_0 + s_1 + s_2 + s_3 \]
>>>take4Sum = NH.sum . take 4 :: Additive a => Stream a -> a>>>simplify $ take4Sum s :: SEs_0+(s_1+(s_2+s_3))
The gradient of this function can be defined as:
>>>:{take4Sum' :: (Distributive a, Distributive (CT a)) => Stream a -> FiniteSupportStream (CT a) take4Sum' = scalarValDerivative take4Sum :}
>>>simplify $ take4Sum' s[1,1,1,1,0,0,0,...
The result is a finite support stream of the form:
\[ 1, 1, 1, 1, 0, 0, 0, \ldots \]
as expected.
Gradinenet over Nested Structured Types
The scalarValDerivative operator can also handle more complex input types.
For example, consider a function g that takes both a 3-vector and a stream:
>>>:{g :: (IntegerPower a, Distributive a) => (BoxedVector 3 a, Stream a) -> a g (v, s) = eNorm2 v + take4Sum s :}
Its gradient can be computed as:
>>>:{g' :: (IntegerPower a, MultiplicativeAction Integer a, Distributive a, CT a ~ a) => (BoxedVector 3 a, Stream a) -> (BoxedVector 3 a, FiniteSupportStream a) g' = scalarValDerivative g :}
Evaluating the gradient at (r, s) gives:
>>>simplify $ fst $ g' (r, s) :: BoxedVector 3 SEVector [2*x,2*y,2*z]
>>>simplify $ snd $ g' (r, s) :: FiniteSupportStream SE[1,1,1,1,0,0,0,...
as expected.
Custom Derivative: Structured Argument Types
The scalarValDerivative operator from the previous section is polymorphic over
the argument type, but it works only for scalar-valued functions.
In this section, we consider how to fix the argument type while keeping the value type polymorphic. This is especially useful when computing second or higher-order derivatives.
Derivatives over a Tuple of Scalars
We begin with a function over a tuple of two scalars, which is equivalent to a function of two arguments.
As an example, consider the product of symbolic functions f and g applied
to separate arguments:
>>>:{x = variable "x" y = variable "y" f :: SymbolicFunc a => a -> a f = unarySymbolicFunc "f" g :: SymbolicFunc a => a -> a g = unarySymbolicFunc "g" h :: (SymbolicFunc a, Multiplicative a) => (a, a) -> a h (x, y) = f x * g y :}
Evaluating h at (x, y) gives:
>>>h (x, y) :: SEf(x)*g(y)
First, consider the derivative operator:
>>>tupleScalarDerivative = customArgValDerivative tupleArg scalarVal
It can be applied as follows:
>>>h' = simplify . tupleScalarDerivative h :: (SE, SE) -> (SE, SE)>>>h' (x, y)(f'(x)*g(y),g'(y)*f(x))
However, we cannot use tupleScalarDerivative to compute the second derivative of h,
because it is restricted to scalar-valued functions. It is not polymorphic in the
value type, unlike tupleArgDerivative.
To define a version suitable for higher-order derivatives, we define:
tupleArgDerivative = customArgValDerivative tupleArg autoVal
This operator is practically equivalent to twoArgsDerivative from the section
Gradient over a Two-Argument Function,
except that it works on uncurried arguments.
We can now compute the derivative of h as:
>>>:{h' :: (SE, SE) -> (SE, SE) h' = simplify . tupleArgDerivative h :}
>>>h' (x, y)(f'(x)*g(y),g'(y)*f(x))
Thanks to the polymorphism of tupleArgDerivative, we can compute higher-order
derivatives of h:
Second derivative:
>>>:{h'' :: (SE, SE) -> ((SE, SE), (SE, SE)) h'' = simplify . tupleArgDerivative (tupleArgDerivative h) :}
>>>h'' (x, y)((f''(x)*g(y),g'(y)*f'(x)),(f'(x)*g'(y),g''(y)*f(x)))
Third derivative:
>>>:{h''' :: (SE, SE) -> (((SE, SE), (SE, SE)), ((SE, SE), (SE, SE))) h''' = simplify . tupleArgDerivative (tupleArgDerivative (tupleArgDerivative h)) :}
>>>h''' (x, y)(((f'''(x)*g(y),g'(y)*f''(x)),(f''(x)*g'(y),g''(y)*f'(x))),((f''(x)*g'(y),g''(y)*f'(x)),(f'(x)*g''(y),g'''(y)*f(x))))
Derivatives over Boxed Vectors
The next example demonstrates derivatives over boxed vectors.
boxedVectorArgDerivative = customArgValDerivative boxedVectorArg autoVal
Recall the function eNorm2, which computes the squared Euclidean norm
of a 3-dimensional vector:
>>>import Numeric.InfBackprop.Utils.SizedVector (BoxedVector)
>>>:{eNorm2 :: Distributive a => BoxedVector 3 a -> a eNorm2 x = foldl' (+) zero (x * x) :}
We apply boxedVectorArgDerivative as follows:
>>>v = DVGS.fromTuple (1, 2, 3) :: BoxedVector 3 Float>>>boxedVectorArgDerivative eNorm2 v :: BoxedVector 3 FloatVector [2.0,4.0,6.0]
The second derivative gives the Hessian matrix represented here as a boxed Vector of boxed Vectors:
>>>boxedVectorArgDerivative (boxedVectorArgDerivative eNorm2) v :: BoxedVector 3 (BoxedVector 3 Float)Vector [Vector [2.0,0.0,0.0],Vector [0.0,2.0,0.0],Vector [0.0,0.0,2.0]]
The third derivative is a rank-3 tensor filled with zeros:
>>>boxedVectorArgDerivative (boxedVectorArgDerivative (boxedVectorArgDerivative eNorm2)) v :: BoxedVector 3 (BoxedVector 3 (BoxedVector 3 Float))Vector [Vector [Vector [0.0,0.0,0.0],Vector [0.0,0.0,0.0],Vector [0.0,0.0,0.0]],Vector [Vector [0.0,0.0,0.0],Vector [0.0,0.0,0.0],Vector [0.0,0.0,0.0]],Vector [Vector [0.0,0.0,0.0],Vector [0.0,0.0,0.0],Vector [0.0,0.0,0.0]]]
How it Works: Structered Argument Types
In order to compute a derivative, we need a function with the following signature:
f :: RevDiff a a -> RevDiff a b
(See section Core type: RevDiff.)
Suppose we want to differentiate a scalar-valued function of a tuple (a, b):
f :: (a, b) -> c
Our strategy is to exploit the polymorphism of f
with respect to the types a and b.
This means that f must also support the type:
f :: (RevDiff t a, RevDiff t b) -> RevDiff t c
To differentiate such a function, we need a way to transform a single input of type
RevDiff a (b0, b1) into a pair of inputs (RevDiff a b0, RevDiff a b1).
This is exactly the role of the argument structure derscriptor:
tupleArg :: (Additive (CT b0), Additive (CT b1)) => RevDiff a (b0, b1) -> (RevDiff a b0, RevDiff a b1)
Using this, we can define a new function:
tupleArg . f :: RevDiff a (b0, b1) -> RevDiff a c
and apply simpleDerivative:
simpleDerivative (tupleArg . f) :: (b0, b1) -> (CT b0, CT b1)
More generally, the expression:
customArgValDerivative arg scalarVal f
is equivalent to:
simpleDerivative (arg . f)
Similarly, we can define argument structure descriptor for Vectors and streams:
boxedVectorArg :: (Additive (CT b), KnownNat n) => RevDiff a (BoxedVector n b) -> BoxedVector n (RevDiff a b)
streamArg :: Additive (CT b) => RevDiff a (Stream b) -> Stream (RevDiff a b)
We can also combine them for more complex structured arguments. For example:
>>>import Numeric.InfBackprop.Utils.SizedVector (BoxedVector)
>>>:{tupleBoxedVectorStreamArg :: (Additive b, Additive c, KnownNat n) => RevDiff a (BoxedVector n b, FiniteSupportStream c) (BoxedVector n d, Stream e) -> (BoxedVector n (RevDiff a b d), Stream (RevDiff a c e)) tupleBoxedVectorStreamArg = cross boxedVectorArg streamArg . tupleArg :}
This allows us to differentiate functions whose arguments have a nested structure,
such as (BoxedVector n a, Stream a).
Alternatively, we can construct argument structure terms using the same style as for value structure terms (see How it Works: Structured Value Types):
>>>:{tupleBoxedVectorStreamArgV2 :: (Additive b, Additive c, KnownNat n) => RevDiff a (BoxedVector n b, FiniteSupportStream c) (BoxedVector n d, Stream e) -> (BoxedVector n (RevDiff a b d), Stream (RevDiff a c e)) tupleBoxedVectorStreamArgV2 = mkTupleArg (mkBoxedVectorArg id) (mkStreamArg id) :}
Note that:
tupleArg = mkTupleArg id boxedVectorArg = mkBoxedVectorArg id streamArg = mkStreamArg id
where id is used for scalar arguments.
Defining Custom Argument Type
To support differentiation with respect to a custom scalar type a,
it is sufficient to define the associated type families:
(See Tangent and Cotangent Spaces for more details.)
Of course, you must also implement some differentiable function, which is to be differentiated, for example:
func :: RevDiff a a -> RevDiff a b
If b is a scalar type,
the derivative will have the type:
func' :: a -> CT a
For structured types like f :: Type -> Type, we recommend the following:
- Define the type families:
- Define the argument type descriptor, which is practically a permutation function:
fArg :: Additive (CT b) => RevDiff a (f b) -> f (RevDiff a b)
- Define the argument type descriptor constructor:
mkFArg :: Additive (CT b) => (RevDiff a b -> c) -> RevDiff a (f b) -> f c
- Provide an instance:
instance (AutoDifferentiableArgument a b c, Additive (CT b)) =>
AutoDifferentiableArgument a (f b) (f c) where
autoArg = mkFArg autoArgFor bifunctor types g :: Type -> Type -> Type:
- Define type families:
- Define the argument type descriptor:
gArg :: (Additive (CT b0), Additive (CT b1)) => RevDiff a (g b0 b1) -> g (RevDiff a b0) (RevDiff a b1)
- Define the argument type descriptor constructor:
mkGArg :: (Additive (CT b0), Additive (CT b1)) => (RevDiff a b0 -> c0) -> (RevDiff a b1 -> c1) -> RevDiff a (g b0 b1) -> g c0 c1
- Provide an instance:
instance (
AutoDifferentiableArgument a b0 c0,
AutoDifferentiableArgument a b1 c1,
Additive (CT b0),
Additive (CT b1)
) =>
AutoDifferentiableArgument a (g b0 b1) (g c0 c1) where
autoArg = mkGArg autoArg autoArgPerformance Remarks
This section discusses performance considerations when using the library.
Subexpression Elimination
Some intermediate results computed during the forward pass (see The Backpropagation Derivative) can be reused during the backward pass. For deep neural networks, this reuse can result in significant computational savings. This optimization can be viewed as a form of subexpression elimination— a problem that Haskell’s evaluation model doesn't always handle automatically.
Consider the following example:
>>>:{f, g, h :: SymbolicFunc a => a -> a f = unarySymbolicFunc "f" g = unarySymbolicFunc "g" h = unarySymbolicFunc "h" k :: BinarySymbolicFunc a => a -> a -> a k = binarySymbolicFunc "k" forwardV1 :: (SymbolicFunc a, BinarySymbolicFunc a, Additive a) => a -> a forwardV1 x_ = k (g y) (h y) where y = f x_ :}
Here we define a function forwardV1 as a composition
of functions. The intermediate result f x is bound to a variable y,
which is then passed to both g and h.
To trace the evaluation of functions f, g, h, and k,
we use the trace function from Debug.Trace.
To facilitate this, we define a traced version Traced
of the symbolic expression type SE:
>>>x = MkTraced $ variable "x" :: Traced SE
For example:
>>>f x :: Traced SE<<< TRACING: Calculating f of x >>> f(x)
The output:
<<< TRACING: Calculating f of x >>>
is produced by the trace mechanism.
Now consider the more complex function:
>>> simplify $ forwardV1 x :: Traced SimpleExpr <<< TRACING: Calculating f of x >>> <<< TRACING: Calculating g of f(x) >>> <<< TRACING: Calculating h of f(x) >>> <<< TRACING: Calculating k of g(f(x)) and h(f(x)) >>> k(g(f(x)),h(f(x)))
The output may vary in order, depending on GHC's optimizations, but importantly,
note that f x is only computed once and its result is reused,
thanks to the local binding.
By contrast, if we define forwardV2
without explicitly factoring out the shared subexpression:
>>>:{forwardV2 :: (SymbolicFunc a, BinarySymbolicFunc a, Additive a) => a -> a forwardV2 x_ = k (g (f x_)) (h (f x_)) :}
the tracing output will show redundant evaluations:
>>> simplify $ forwardV2 x :: Traced SimpleExpr <<< TRACING: Calculating f of x >>> <<< TRACING: Calculating g of f(x) >>> <<< TRACING: Calculating f of x >>> <<< TRACING: Calculating h of f(x) >>> <<< TRACING: Calculating k of g(f(x)) and h(f(x)) >>> k(g(f(x)),h(f(x)))
Here, f x is computed twice.
This illustrates that GHC does not always automatically eliminate subexpressions.
Now consider tracing the derivative of forwardV1.
In the long output below, observe that f'
is not computed twice during the backward pass:
>>> simplify $ simpleDerivative forwardV1 x :: Traced SimpleExpr <<< TRACING: Calculating f' of x >>> <<< TRACING: Calculating f of x >>> <<< TRACING: Calculating g' of f(x) >>> <<< TRACING: Calculating g of f(x) >>> <<< TRACING: Calculating h of f(x) >>> <<< TRACING: Calculating k'_1 of g(f(x)) and h(f(x)) >>> <<< TRACING: Calculating (*) of k'_1(g(f(x)),h(f(x))) and 1 >>> <<< TRACING: Calculating (*) of g'(f(x)) and k'_1(g(f(x)),h(f(x)))*1 >>> <<< TRACING: Calculating (*) of f'(x) and g'(f(x))*(k'_1(g(f(x)),h(f(x)))*1) >>> <<< TRACING: Calculating h' of f(x) >>> <<< TRACING: Calculating k'_2 of g(f(x)) and h(f(x)) >>> <<< TRACING: Calculating (*) of k'_2(g(f(x)),h(f(x))) and 1 >>> <<< TRACING: Calculating (*) of h'(f(x)) and k'_2(g(f(x)),h(f(x)))*1 >>> <<< TRACING: Calculating (*) of f'(x) and h'(f(x))*(k'_2(g(f(x)),h(f(x)))*1) >>> <<< TRACING: Calculating (+) of f'(x)*(g'(f(x))*(k'_1(g(f(x)),h(f(x)))*1)) and f'(x)*(h'(f(x))*(k'_2(g(f(x)),h(f(x)))*1)) >>> (f'(x)*(g'(f(x))*k'_1(g(f(x)),h(f(x)))))+(f'(x)*(h'(f(x))*k'_2(g(f(x)),h(f(x)))))
The possible duplication of becomes more severe as function composition grows deeper— a major performance issue in neural network applications.
For further illustration, consider the first and second derivatives
of the composition (g . f):
>>> simpleDerivative (g . f) x :: Traced SimpleExpr <<< TRACING: Calculating f' of x >>> <<< TRACING: Calculating f of x >>> <<< TRACING: Calculating g' of f(x) >>> <<< TRACING: Calculating (*) of g'(f(x)) and 1 >>> <<< TRACING: Calculating (*) of f'(x) and g'(f(x))*1 >>> f'(x)*(g'(f(x))*1)
>>> simpleDerivative (simpleDerivative (g . f)) x :: Traced SimpleExpr <<< TRACING: Calculating f'' of x >>> <<< TRACING: Calculating f of x >>> <<< TRACING: Calculating g' of f(x) >>> <<< TRACING: Calculating (*) of g'(f(x)) and 1 >>> <<< TRACING: Calculating (*) of g'(f(x))*1 and 1 >>> <<< TRACING: Calculating (*) of f''(x) and (g'(f(x))*1)*1 >>> <<< TRACING: Calculating f' of x >>> <<< TRACING: Calculating g'' of f(x) >>> <<< TRACING: Calculating f' of x >>> <<< TRACING: Calculating (*) of f'(x) and 1 >>> <<< TRACING: Calculating (*) of 1 and f'(x)*1 >>> <<< TRACING: Calculating (*) of g''(f(x)) and 1*(f'(x)*1) >>> <<< TRACING: Calculating (*) of f'(x) and g''(f(x))*(1*(f'(x)*1)) >>> <<< TRACING: Calculating (+) of f'(x)*(g''(f(x))*(1*(f'(x)*1))) and 0 >>> <<< TRACING: Calculating (+) of f''(x)*((g'(f(x))*1)*1) and (f'(x)*(g''(f(x))*(1*(f'(x)*1))))+0 >>> (f''(x)*((g'(f(x))*1)*1))+((f'(x)*(g''(f(x))*(1*(f'(x)*1))))+0)
Here we observe that f'(x) is computed twice in the second derivative.
This occurs because it appears in two different branches of the expression tree:
once as the outer derivative, and once via the inner term g'(f(x)).
Unfortunately, the current implementation of simplify is not able to eliminate
this redundancy, as it lacks full common subexpression elimination.
Nevertheless, for typical neural network applications, the current backpropagation implementation for the first derivative is performant enough in practice.
Forward Step Results Reusage
Some results from the forward pass can be reused during the backward pass, leading to significant computational savings. Let's explore this optimization through a concrete example.
Consider differentiating the hyperbolic functions:
\[ \cosh x = \sinh' x = \frac{e^x + e^{-x}}{2} \] and \[ \sinh x = \cosh' x = \frac{e^x - e^{-x}}{2} \]
Notice that both functions require computing the same exponentials: \(e^x\) and \(e^{-x}\). During the forward pass, we calculate these exponentials to compute the function value. Then, during the backward pass for derivative computation, we need exactly the same exponentials again. Rather than recomputing them, we can reuse the forward pass results.
This optimization becomes particularly valuable when dealing with computationally expensive operations, such as matrix exponentials, where avoiding redundant calculations can dramatically improve performance.
While automatic subexpression elimination techniques exist, we'll explore a different approach: manual subexpression elimination implemented directly in the backpropagation definition. This gives us explicit control over which intermediate results to preserve and reuse.
Here's how we implement this optimization:
We define an ExpFieldV2 typeclass that produces the same function values as
ExpField
but differs in how it handles intermediate computations, specifically designed to
enable result reuse:
>>>:{class ExpFieldV2 a where expV2 :: a -> a sinhV2 :: a -> a coshV2 :: a -> a instance ExpFieldV2 SE where expV2 = exp sinhV2 x_ = (exp x_ - exp (negate x_)) / number 2 coshV2 x_ = (exp x_ + exp (negate x_)) / number 2 instance (ExpFieldV2 a, Distributive a, Subtractive a, Divisive a, FromInteger a) => ExpFieldV2 (RevDiff t a a) where expV2 = simpleDifferentiableFunc expV2 expV2 sinhV2 (MkRevDiff x bpc) = MkRevDiff ((expP - expM) NH./ fromInteger 2) (bpc . ((expP + expM) *)) where expP = expV2 x expM = expV2 (negate x) coshV2 (MkRevDiff x bpc) = MkRevDiff ((expP + expM) NH./ fromInteger 2) (bpc . ((expP - expM) *)) where expP = expV2 x expM = expV2 (negate x) instance (ExpFieldV2 a, ExpField a, FromInteger a, Show a) => ExpFieldV2 (Traced a) where expV2 = addTraceUnary "exp" expV2 sinhV2 x_ = (expV2 x_ - expV2 (negate x_)) / fromInteger 2 coshV2 x_ = (expV2 x_ + expV2 (negate x_)) / fromInteger 2 :}
The key insight is in the RevDiff instance: we manually store the exponentials
expP (for \(e^x\)) and expM (for \(e^{-x}\)) as local bindings.
This ensures they're
computed only once and then reused both for the forward value calculation and
the backward pass derivative computation.
Let's verify this optimization works as expected by tracing the computations:
>>>x = MkTraced $ variable "x" :: Traced SE
>>> coshV2 x <<< TRACING: Calculating exp of x >>> <<< TRACING: Calculating negate of x >>> <<< TRACING: Calculating exp of -(x) >>> <<< TRACING: Calculating (+) of exp(x) and exp(-(x)) >>> <<< TRACING: Calculating (/) of exp(x)+exp(-(x)) and 2 >>> (exp(x)+exp(-(x)))/2
Now let's examine what happens when we compute both the value and derivative.
To this end, we use a function simpleValueAndDerivative
that computes both the value and derivative:
>>> simpleValueAndDerivative coshV2 x :: (Traced SE, Traced SE) ( <<< TRACING: Calculating exp of x >>> <<< TRACING: Calculating negate of x >>> <<< TRACING: Calculating exp of -(x) >>> <<< TRACING: Calculating (+) of exp(x) and exp(-(x)) >>> <<< TRACING: Calculating (/) of exp(x)+exp(-(x)) and 2 >>> (exp(x)+exp(-(x)))/2, <<< TRACING: Calculating (-) of exp(x) and exp(-(x)) >>> <<< TRACING: Calculating (*) of exp(x)-exp(-(x)) and 1 >>> (exp(x)-exp(-(x)))*1)
Notice how the exponential calculations (exp of x and exp of -(x)) appear only once in the trace, even though they're used in both the forward and backward passes. This demonstrates that our manual subexpression elimination successfully avoids redundant computations, reusing the exponential results as intended.
Moreover, we can compute the second derivative without recomputing the exponentials:
>>> simpleDerivative (simpleDerivative coshV2) x :: Traced SE <<< TRACING: Calculating exp of x >>> <<< TRACING: Calculating (*) of 1 and 1 >>> <<< TRACING: Calculating (*) of exp(x) and 1*1 >>> <<< TRACING: Calculating negate of x >>> <<< TRACING: Calculating exp of -(x) >>> <<< TRACING: Calculating negate of 1*1 >>> <<< TRACING: Calculating (*) of exp(-(x)) and -(1*1) >>> <<< TRACING: Calculating negate of exp(-(x))*-(1*1) >>> <<< TRACING: Calculating (+) of exp(x)*(1*1) and -(exp(-(x))*-(1*1)) >>> <<< TRACING: Calculating (+) of (exp(x)*(1*1))+-(exp(-(x))*-(1*1)) and 0 >>> ((exp(x)*(1*1))+-(exp(-(x))*-(1*1)))+0
What is Next
Unboxed vectors and tensors are not currently supported in the library.